Research colloquia (Titles partially in German):
Numerical mathematics
Dynamischer Seminarplan des Forschungskolloquiums Numerische Mathematik
Mittwoch, 15:15 - 16:45, Raum 326/327 (alternativ 427 oder irgendwo im Netz via zoom/jitsi)
Wintersemester 2023
- 06.12.2023 13:30 Uhr Jan Hellwig (Uni Rostock):
Fortschritsbericht - 18.12.2023 14:00 Uhr Willi Gerbig (Uni Rostock):
Modellierung und Steuerung eines Einraum-Heizsystems - 31.01.2024 15:00 Uhr Martina Beese (Uni Rostock):
Nichtnegative Faktorisierungstechniken für unvollständige Datensätze
Wintersemester 2021
- 14.10.2021 09:15 Uhr: Martina Beese (Uni Rostock):
Ein geometrisches Maximumsprinzip für die Evolving Factor Analysis - 05.11.2021 11:00 Uhr: Tomass Andersons (Uni Rostock):
Advances in rank-deficient problems - 16.12.2021 10:00 Uhr: Tomass Andersons (Uni Rostock):
Advances in rank-deficient problems
Wintersemester 2020
- 10.03.2021 15:15 Uhr: Denise Meinhardt (Uni Rostock):
Projektfortschrittsbericht (Pfadverfolgung und Profilanpassung) - 17.03.2021 15:15 Uhr: Martina Beese (Uni Rostock):
Projektfortschrittsbericht (Pure variables). - 24.03.2021 15:15 Uhr: Tomass Andersons (Uni Rostock):
Projektfortschrittsbericht (Rangdefizitprobleme) - 31.03.2021 15:15 Uhr: Mathias Sawall (Uni Rostock):
Quadrilaterale Hauptüberdeckungen und sporadische Extravertices.
Sommersemester 2020
- 01.04.2020 15:15 Uhr: Willi Gerbig (Uni Rostock):
Fortschrittsbericht - 17.06.2020 17:00 Uhr: Christian Bahls (MathCom):
Differentiable Programming
Application to Motion Planning
Teilnahme via jitsi.
Wintersemester 2019
- 23.10.2019 15:00 Uhr: Anton Evgrafov (TU Denmark):
Nonlocal optimal control in the conduction coefficients:
a bit of theory and practice - 06.11.2019 11:55 Uhr: Willi Gerbig (Uni Rostock):
Projektstandsbericht - 02.12.2019 14:00 Uhr: Michael Maiwald (BAM):
Informationsmanagement in der Prozessindustrie auf Basis von Labor- und Produktionsdaten. - 13.12.2019 11:30 Uhr: Bahram Hemmateenejad (University of Shiraz):
Hard-soft modelling by Net analyte signal - 18.12.2019 Pseudo-periodic recurrences (Cristmas)
- 22.01.2020 15:15 Uhr: Thomas Ihle (Uni Greifswald):
Kinetic theory of self-propelled particles - 31.01.2020 15:15 Uhr: Ming Zhou (UR):
Krylovraum-basierte Eigenlöser für elliptische Differentialoperatoren
Sommersemester 2019
- 14.03.2019 10:00 Uhr, Hörsaal 427, Konstantinos Spiliotis (Athens):
Equation Free Computations on Neuronal Networks:
From Neuronal Interactions To Emergent Brain Dynamics - 07.03.2019 14:00 Uhr, Hörsaal 326, Annalisa Iuorio (TU Wien):
Geometric Singular Perturbation Analysis of a
Model for Micro-Electro Mechanical Systems (MEMS) - 01.04.2019 17:00 Uhr, Hörsaal 001 „August Michaelis“ des Instituts für Chemie (Albert-Einstein-Straße 3a):
Mathias Sawall (Uni Rostock): Über mathematische Verfahren zur Spektrenanalyse mittels Faktormethoden
(Habilitationskolloquium) - 03.04.2019 10:00 Uhr: Marcel Maeder (University of Newcastle, Australia):
Chemo Metrics, das Zusammenspiel zwischen Chemie und Metrie - 11.04.2019 16:00 Uhr: Wolfram Just (Queen Mary University of London) :
Transfer operator technique for analytic maps - Or: Chaos in the Hilbert space - 07.05.2019 10:00 Uhr: Matthias Rüdt (Karlsruher Institut für Technologie (KIT)):
Bilinear Data Sets in Biopharmaceutical Process Development:
From Process Spectroscopic Data to Reference Analytics - 08.05.2019 15:15 Uhr: Kristina Kowalski (Uni Rostock)):
Hydrostatic pressure, salinity and temperature:
An experimental approach - 19.06.2019 15:15 Uhr, Raum 427: W. Gerbig (Rostock):
Fortschrittsbericht - 05.07.2019 15:15 Uhr, Hörsaal 1 der Physik (Albert-Einstein-Str. 24) : D. Langemann (Braunschweig):
Schwingungen, Klänge und Geometrie.
Sommerfest der Mathematisch-Naturwissenschaftlichen Fakultät
Mathematical institute
Fields of activity:
- Nonnegative matrix factorizations, factor analysis
- Numerical linear algebra
- Preconditioned solvers for eigenvalue problems of partial differential operators
- Scientific Computing
- Equation free modeling
- Approximation theory
- Wavelets and digital image processing
- Mathematical modeling and simulation
- Configuration flow problems
List of publications:
Research projects in recent years:
Research Training Group RTG 2943 (DFG 2024-2029)
Collaboration in the Research Training Group 2943 "Spectroscopic tools for challenging reduction reactions- catalytic coupling of CO2" (SPECTRE)
Sharp a priori convergence estimates for Krylov subspace eigensolvers (DFG 2021-2023)
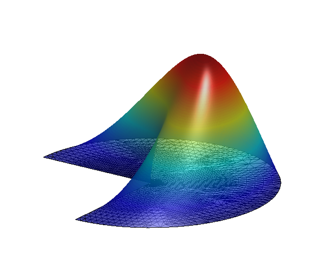
Eigenvalue problems of elliptic and self-adjoint differential operators occur in various scientific and technical applications. Their numerical solution succeeds by means of an adaptive finite element discretization and the iterative computation of the desired eigenpairs of the discretized operators. Subspace iterations are well known to be fast solution methods for the high-dimensional matrix eigenvalue problems and are considerably more efficient than classical diagonalization methods. Popular subspace iterations work in Krylov subspaces and can be understood as improved variants of the almost 70 years old Lanczos method. The main procedural variants include restarts, blockwise implementation and preconditioning. The associated convergence theory has not been able to keep pace with the active development of new procedural variants. In addition, many convergence estimates have an a posteriori character, i.e. they bound the rates of convergence by means of complicated formula that depend on the (to be) calculated Ritz values.The proposed project deals with new approaches for the convergence analysis of Krylov subspace iterations for real and symmetric matrix eigenvalue problems. First of all, four basic iteration methods are analyzed: standard Krylov subspace iterations, restarted Krylov subspace iterations, block-Krylov subspace iterations, and restarted block-Krylov subspace iterations. The resulting estimates should lead to an improved understanding of the convergence behavior of these subspace iterations. An extension to the related preconditioned iterations is planned. One focus is on a priori estimates, which can be derived under rather weak assumptions and work with less complex bounds. Probabilistic techniques have a high potential for deriving realistic convergence rates and will be combined with geometric interpretations of Rayleigh quotient level sets and preconditioning. New adaptive control techniques for the block numbers and block sizes suggest a gain in efficiency, which should be demonstrated for application problems such as the self-consistent field iterations in the quantum mechanical density functional theory
Numerical methods for the computation of mutli-component decompositions with spectroscopic applications (DFG 2012-2020)
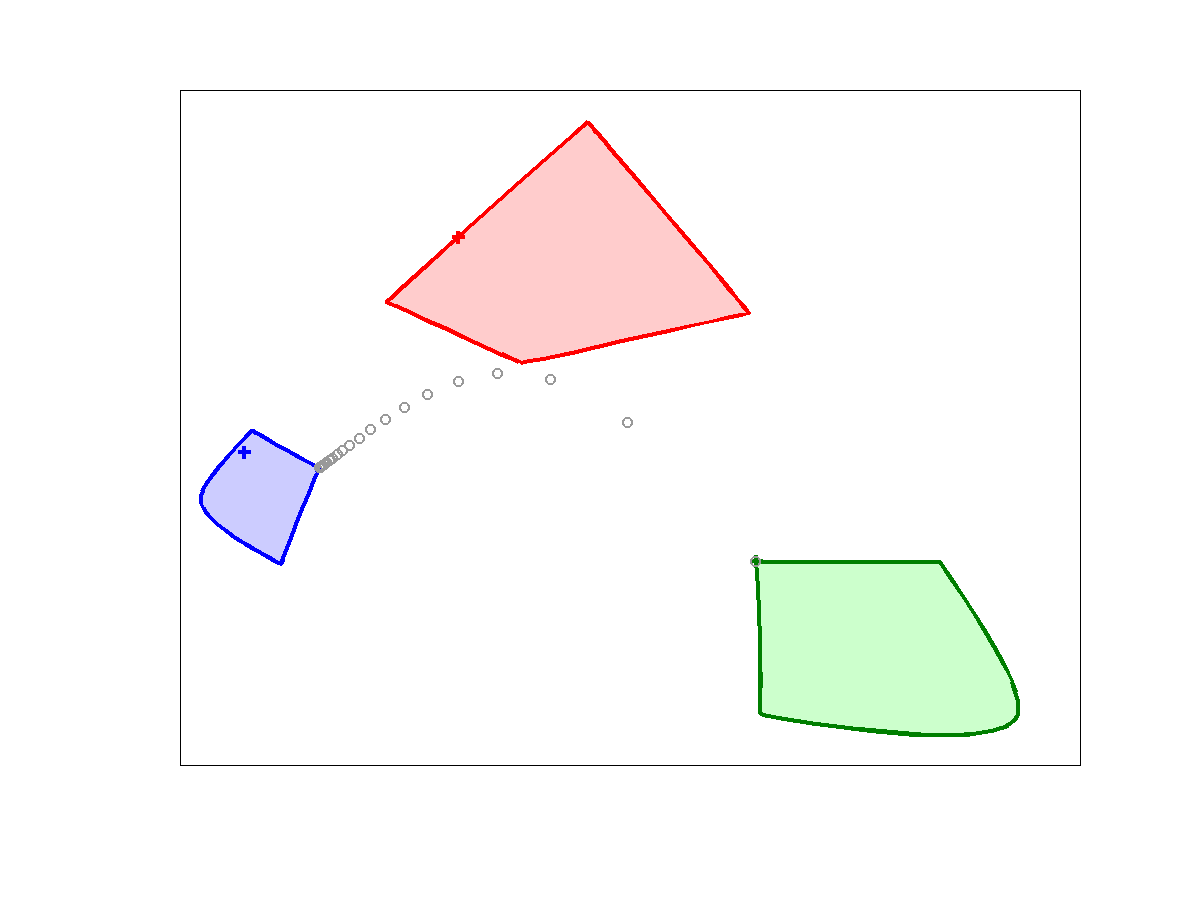
The spectroscopic observation of chemical reactions with high frequency resolution and a large number of spectra results in a high volume of data. These spectral data contain the superposed contributions from the pure components. Factor analytic methods of chemometrics allow to extract from these data the number of underlying pure components, their spectra and the associated concentration profiles. New mathematical techniques and new numerical solution methods for the factor analysis of multicomponent systems are under development in the current funding period of the project. Whereas the so-called self-modeling factor analytic methods in chemometrics generally suggest only a single feasible pure component decomposition, our new systematic approach allows to compute the full set of all feasible solutions. Further methods have been developed in order to identify the correct pure component factorization for instance by coupling with a kinetic model of the reaction or by the new complementarity theory. The fast and stable numerical solvers have been published in the FAC-PACK software. Our work primarily aims at the development of chemometric methods but is also accompanied by a close cooperation with the Leibniz-Institute for Catalysis e.V. in Rostock. Spectroscopic data for various chemical reaction systems with the focus on transition metal catalyzed carbonylation reactions have been used for the validation of the numerical methods. Significant progress has been made for in-situ FT-IR studies on reaction systems of homogeneous catalysis.
List of third-party funded research projects:
Please press the button "Projects" or click here.
Software projects
- FACPACK - software for computation of multi-component factorizations and the area of feasible solutions:
- Adaptive Multigrid Preconditioned Eigensolver: A software for the computation of the smallest eigenvalues and the associated eigenfunctions of a self-adjoint and elliptic partial differential operator in 2D domains.